[고려대학교 IME654] 01-3: Dimensionality Reduction

[Korea University] Business Analytics (Graduate, IME654)
Dimensionality Reduction - Genetic Algorithm
1장: Dimensionality Reduction
Part 3: 변수 선택 기법: 유전 알고리즘

이번 포스트는 지도 학습 (supervised learning) 기반 Dimensionality reduction의 두 번째 파트로 genetic algorithm을 이용한 변수 선택 방법에 대해 설명하도록 하겠습니다. 본 내용은 고려대학교 강필성 교수님의 2020년도 2학기 일반대학원 산업경영공학과 비즈니스 애널리틱스 (IME654) 강의를 정리하였으며, 사용된 사진 또한 수업의 강의 자료 (github.com/pilsung-kang/Business-Analytics-IME654-)를 활용하였습니다.

앞서 지난 포스트에서 설명했던 방법론들에 대한 간략한 review를 해보도록 하겠습니다.

Exhaustive Search: optimal subset을 보장해주지만 너무나도 오랜 시간이 걸려서 사용하는 것이 현실적으로는 불가능하다.
Local Search (forward/backward/stepwise): 효과적인 search 방법이지만 ES에 비해 search 범위가 너무 제한적이기 때문에 optimal solution에 도달할 확률이 확연히 낮다

Local Search의 한계점에 따라, 소요시간을 조금 더 들더라도 search 범위를 넓혀 성능을 향상하고자 하는 Genetic Algorithm을 이용한 변수 선택 방법을 소개하도록 하겠습니다.

Genetic Algorithm은 Metaheuristic approach와 깊은 관련이 있습니다. 효율적으로 trial-and error을 해가면서 최적의 해결책을 찾아내는 것이 핵심입니다. Metaheuristic 방법론 중에서는, 자연현상이 어떻게 일어나는지 파악한 다음 그걸 모사한 알고리즘이 여럿 있습니다: Artificial Neural Network, Ant Colony Algorithm, Particle Swarm Optimization.

Artificial Neural Network (인공신경망): 기계학습과 인지과학에서 생물학의 신경망(동물의 중추신경계 중 특히 뇌)에서 영감을 얻은 통계학적 학습 알고리즘으로, 뇌의 구조와 동작 방식을 모방하여 이를 수학적으로 모델링한 것입니다.
Ant Colony Optimization Algorithm (ACO): 컴퓨터를 이용해 연결 그래프의 최적의 길을 찾는 방법을 줄일 수 있는 알고리즘으로, 계산문제를 푸는 확률적 해법 중 하나로 그래프에서 최적의 경로를 찾는 데 쓰입니다. 개미가 개미집에서 먹이로의 경로를 찾을 때, 먹이를 발견한 첫 개미가 페로몬을 남기며 집으로 돌아옵니다. 다음 개미는 역시 페로몬을 뿌리면서 앞선 개미의 페로몬을 따라 먹이를 찾는데, 중간중간 희미한 페로몬 때문에 경로가 조금씩 바뀌기도 하면서 여러 가지 경로가 쌓입니다. 페로몬은 시간이 지나면서 증발하고 결국 최적의 경로에만 페로몬이 남게 됩니다. 이러한 개미의 집단행동에서 아이디어를 얻어 이를 모사한 알고리즘입니다.
Particle Swarm Optimization (PSO): 사회적 행동 시뮬레이션을 시도하는 반복적인 최적화 알고리즘입니다. 새가 대열을 만들어서 무리 지어 날아다니는 게 그냥 날아다니는 게 아니라, 이게 가장 에너지를 적게 소모하면서 멀리 날아갈 수 있는 대형이라고 합니다.
AlphaStar: Mastering the Real-Time Strategy Game StarCraft II: meta-heuristic approach에 의해서 개발된 것이다. 'alphastar: an evolutionary computation perspective' 논문에 보시면 Lamarkian evolution이라는 용어가 나옵니다. 이건 다윗의 자연선택설 라마르크의 용불용설 이런 게 있는데,, 현대에서는 지금 다윗의 자연선택설이 헤게모니를 쥐고 있습니다. 이건 생존에 유리한 객체들이 남아서 후대에 그걸 물려주었다는 것입니다. 용불용설은 목을 자꾸 길게 뻗다 보니까 기린이 긴 목을 가지게 되었다는 것.

이 중 오늘 설명할 GA를 이용한 변수 선택은 자연선택설에 기반한 방법론으로, 정확하게는 자연선택설과 포유류의 생식 process를 모방한 알고리즘입니다. 이 모방하는 과정에서 무얼 하는 거냐면, 반복적인 세대의 재생산을 통해서 가장 좋은 솔루션을 찾는 것입니다. 좋은 솔루션을 찾기 위한 genetic algorithm의 핵심적인 세 가지 요소는 다음과 같습니다: selection, crossover, mutation. 각각이 하는 역할을 뒤에서 다시 자세하게 설명하도록 하겠습니다. 간략하게 세 가지 요소를 설명하자면,

selection: solution의 quality를 높일 수 있는 후보군을 찾는 데에 집중
crossover(교배): 앞선 세대에 quality 가 우수한 객체들을 이용해서 유전자들을 섞어가면서 더 나은 대안이 있는지를 탐색
mutation(돌연변이) : 수렴하는 과정에서 혹시나 local optimum으로 수렴하게 된다면 그 경우에 local optimum에서 빠져나와서 global optimum으로 갈 수 있도록 해주는 것.

Genetic algorithm을 통한 변수 선택은 크게 6가지 단계로 이루어진다.

1) 염색체를 초기화하고 파라미터를 설정하는 initiation 단계. 2) 두번째 단계는 염색체 별로 대응하는 변수들만을 사용해서 예측 모형을 학습하는 단계. 3) 학습된 모델에 대해서 적합도를 평가. 4) 적합도 평가를 통해서 우수 염색체들을 선택. 5) 선택된 염색체들을 통해서 다음 세대 염색체들을 생성.

핵심은 여기 feedback loop에 있습니다. 5단계에서 2단계로 돌아가는 과정을 ‘세대’라고 표현하는데, generation이 수행되었다라고 표현합니다. 세대가 진화함에 따라서 quality가 상승하고, 충분히 많은 횟수동안 반복을 해서 더 이상 성능 향상이 없을 때 최종적으로 6단계 최종 변수 집합을 선택하게 됩니다.

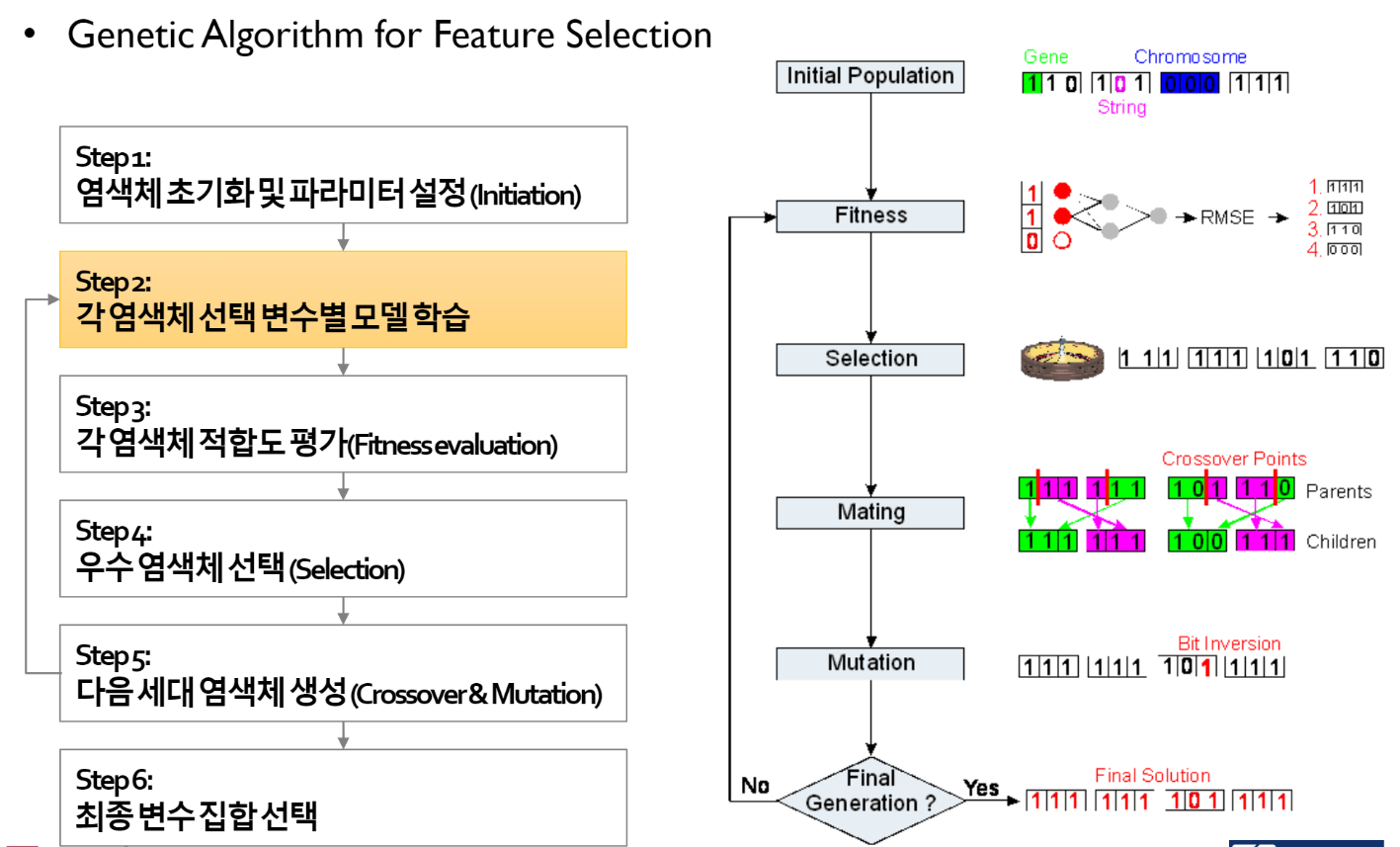
각 단계에 대해서 자세히 설명하도록 하겠습니다.

GA step 1: Initialization (초기화 단계)

Genetic algorithm은 변수 선택은 genetic algorithm이 활용되는 한 가지 사례에 불과하고, 훨씬 더 많은 범위의 최적화 문제에서 사용될 수 있습니다. 그때 사용되는 task에 따라고 encoding scheme이 달라집니다. 유전 알고리즘인 만큼 용어들도 유전학에 쓰이는 용어들이 그대로 사용되며, 염색체에 해당하는 'chromosome을 인코딩한다'라고 표현합니다. 위에 보이는 그림에서 vector가 chromosome, cell은 gene이라고 하게 됩니다. 염색체는 d차원의 vector로 사용이 되고, X가 d차원의 데이터이면 이 chromosome은 d-차원의 binary vector가 됩니다 (d-dimensional binary vector). 각각의 cell을 유전자 (gene)이라는 용어로 지칭하게 되는데, 이때 binary vector이기 때문에 0 또는 1의 값이 들어가게 됩니다.

0 = 그 위치에 해당하는 변수를 모델링에 사용해라
1 = 그 위치에 해당하는 변수를 모델링에 사용하지 말아라

위의 그림에서는 binary vector로 encoding 된 chromosome에서 숫자 1의 값을 가지고 있는 vector의 위치에 대응하는 변수들, 즉 $x_1$, $x_4$, $x_6$, $x_7$, $x_d$를 모델링에 사용하라는 뜻이 된다.

유전 알고리즘의 Hyperparameter는 다음과 같다.

Parameter Initialization

The number of chromosome (population): 한 세대에서 몇 개의 chromosome을 생성해서 갖고 갈 것인가. 만약 100으로 설정했다면 한 세대에서 100개의 변수 부분집합(조합)을 평가하겠다는 얘기다. chromosome하나 당 subset 하나가 나오니까 100개의 subset을 평가하겠다는 것이다.
fitness function: 각각의 chromosome이 얼마나 뛰어난가, 즉 chromosome의 quality를 평가하는 것이다.
crossover mechanism: 교배 방식
the rate of mutation: 돌연변이율
stopping criteria: 종료 조건. 두 가지가 있는데 둘 중 하나만 OR 조건으로 사용

위에 보이는 figure의 그래프 x축이 generation, y축이 fitness value입니다. 초록색은 best chromosome에 의해서 선택된 변수들의 예측 성능입니다. 하늘색은 해당하는 세대의 chromosome들의 평균입니다. 여기서 선택된 변수들의 예측 성능이라고 하면, 어떤 chromosome이 5차원이라고 가정하고. encoding이 아래와 같이 되어있다고 가정하면,

다중 선형 회귀분석으로 표현을 하면 이 chromosome을 통해서 이런 모델을 만들 수가 있게 됩니다.

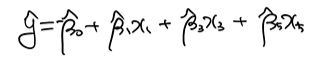
이렇게 만들어낸 모델에 대해서 $R_adj^2$값이 0.78이 나왔다고 하면, 이 chromosome의 fitness function value가 0.78이라고 이해하면 됩니다. 그럼 chromosome에 encoding이 되어있는 binary vector들이 다 다를 테니까, 그 조합들에 대해서 fitness function value가 다 따로따로 다르게 나오게 되는 것입니다.

예시)

아래 그림은 10차원의 설명변수에 대해서 chromosome을 8개를 만든 예시입니다. cutoff를 0.5로 두어서 0과 1의 binary vector를 변환해야 합니다.이게 population을 initialization을 하고 chromosome에 대한 binary vector를 생성하는 과정입니다.

그다음, 생성한 binary vector 정보를 기반으로 모델을 만듭니다. 우선 가장 먼저 chromosome1에 대한 모델을 만들어 보았습니다.

이런 식으로 chromosome 8개에 대해서 모델을 만들게 되면, 8개의 다중선형회귀분석을 학습하게 되는 것입니다.

GA step 3: Fitness Evaluation

다음으로는 적합도 함수(fitness function)를 사용하여 도출한 값을 평가하게 됩니다. 다시 말하면, 어떤 chromosome이 더 좋은가를 평가하는 기준이 됩니다. Fitness function의 값은, 정확도와 같이, 높은 값을 가질수록 우수한 chromosome이라고 정의할 수 있습니다. 그래서 회귀모형 같은 경우에 error율이 낮은 걸 fitness function으로 하고 싶다면, error율을 fitness function으로 하는 것이 아니라 '1-error율'을 fitness function으로 설정해야 하는 것입니다.

또한 fitness evaluation을 할 때는 다음과 같은 criteria들이 반영이 되어야 합니다.

만약 동일한 예측성능(performance)을(performance) 가지고 있다면, 변수의 수가 적은 것을 더 높게 판단해라 (preferred)
같은 변수의 개수를 가지고 있다면 더 높은 예측성능(performance)을 더 높게 판단하라 (preferred

앞선 예시를 이어서 사용하여 8개의 chromosomes들의 $R_adj^2$값을 fitness function으로 사용했습니다. 이제 두 가지 task를 수행해야 하는데, 일단 처음으로 rank를 매기고, 가중치(weight)를 계산합니다.

"가중치(weight) = $R_adj^2$값/전체 chromosome의 fitness function값들의 SUM"으로 계산될 수 있으며, 첫 번째 chromosome1 같은 경우에는 0.75/(0.75+0.78+0.50+0.65+0.40+0.35+0.25+0.55) = 0.177 다음과 같이 구할 수 있다. 이 weight 값은 crossover 단계에서 중요하게 사용됩니다.

여기까지 해서 chromosome modeling을 수행했고, fitness function을 적용해서 평가를 했습니다. 그다음은 selection 단계입니다. 이 단계에서는 chromosome을 선택하게 되는데,

두 가지 방법이 있습니다.

1. Deterministic Selection | 상위 n%에 해당하는 chromosome 들만 다음 세대에 유전자를 넘길 수 있는 기회를 줌.

2. Probablistic Selection | 앞선 deterministic selection 방법에 따르면, 상위 50%한테만 기회를 부여한다고 치면 rank로 1~4등만 주겠다는 뜻인데, 4위와 5위가 차이가 거의 나지 않을 수도 있기 때문에 너무 가혹한 selection 방법이다. 가중치(weight)를 이용해서 1~8등에게 모두 기회를 준다. 다만 random number initialization을 통해 chromosome selection이 이루어지기 때문에 weight가 낮은 건 선택 될 chance도 낮고, weight가 높으면 선택될 확률 또한 chance도 높음. 결국 weight는 fitness value에 의해서 결정되기 때문에, 이에 따라서 기회를 더 주고 덜 주고 하게 되는 것.

GA step 5: crossover & mutation

Crossover

사람은 46개의 염색체를 가지고 있고, 자식들은 이렇게 나오게 되는데, 이 과정을 그대로 모사한 것이다.

그림에서 보이는 것과 같이 부모 chromosome에서 절반씩의 정보를 가져와서 자식 chromosome을 만드는 것입니다. 근데 여기서도 hyperparameter가 crossover point라는 게 있습니다. 부모 chromosome에서 어느 지점에서 끊어서 가져올 것인가입니다.

crossover point는 1개 이상이 될 수 있는데, 아래 그림에서 보이는 것처럼 crossover point가 하나라면 5와 6 사이로 정해졌으면, x1~x5는 chromosome 4에서 가져오고 6~10은 chromosome 8을 가져오는 이런 식으로 child를 생성하게 됩니다. crossover point는 1개 이상이 될 수 있는데, 아래 그림은 crossover point가 한 곳일 때입니다.

2 crossover points

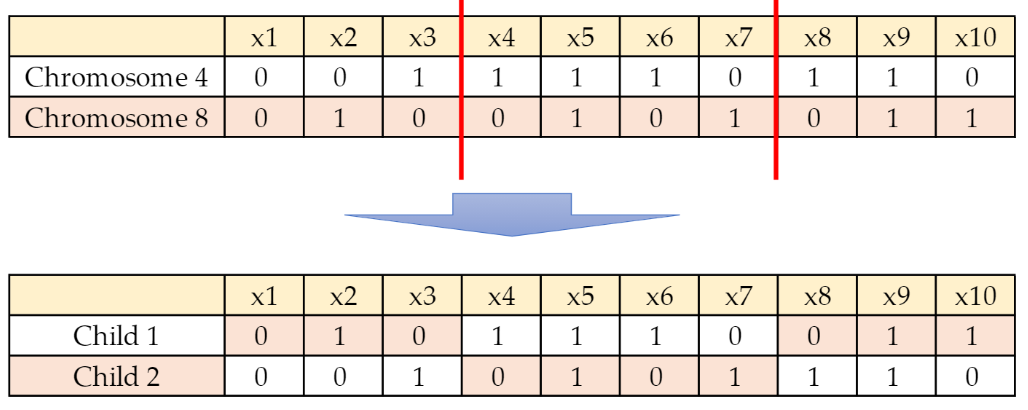
10 crossover points

이런 식으로 부모 chromosome의 gene 정보들을 적절히 잘라서 섞는 게 crossover(교배) 단계입니다. 이걸 극단적으로 생각하면 모든 point에서 crossover가 일어날 수 있습니다.

이제 random number를 생성을 해서 0.5보다 큰 건 생성을 해주고 아닌 것은 하지 않습니다. selection의 reproduction과정에서 가장 자유도가 높은 걸 생각해보면, deterministic 방식이 probablistic 방식이 자유도가 높고, crossover 방식은 1에서 10으로 갈수록 자유도가 높아진다는 얘기입니다. (자유도가 높아진다고 좋다는 것을 의미하지는 않습니다.)

Mutation (돌연변이)

만약 chromosome들이 생성이 되면서 local optimum을 향해 가고 있다면, global optimum을 찾을 수 있도록, 즉 local optimum에서 빠져나올 수 있도록 기회를 제공하는 것이다.

유의해야 할 점은 지나치게 큰 mutation을 rate로 사용하게 되면, converge(수렴)하는 데에 있어서 시간을 길게 증가시킬 수 있다는 점입니다. 말 그대로 돌연변이는 확률이 높은 게 아니라 낮기 때문에 실질적으로 알고리즘을 돌릴 때는 0.01 미만으로서 굉장히 낮은 값을 잡게 됩니다.

예시를 통해서 살펴보면, 각각의 crossover를 통해서 만들어진 두 개의 child node에 대해서 역시 또 난수를 생성합니다. 이 중에 0.01보다 낮은 값은 딱 한 군데, 그럼 이걸 0으로 변환을 해줍니다 (flip). 여기서 child2의 9번 choromosome에 대해서만 mutation이 수행이 된 것이고, 나머지는 mutation이 되지 않도록 설정이 되었기 때문에 그대로 원래 값을 가지고 있게 되는 것입니다.

결론적으로 전체적인 과정은 좋은 chromosome을 선택하고, 후보 부모들을 선택하고, 부모로부터 crossover와 mutation을 통해서 자식들을 생성하는 것이 핵심입니다. 이 과정을 반복하며 chromosome 중에 가장 높은 fitness function을 가지고 있는 best solution(best subset)을 찾습니다. 아래 그림을 통해 알 수 있듯이, 이 distance라는 개념은 낮을수록 좋은 것이기 때문에 그래프에서 보이는 genetic algorithm performance가 아래로 갈수록 향상되고 있음을 의미합니다. 500번의 generation (iteration*10)에서 초반에는 fitness value의 향상이 급격하게 이루어집니다. 그러다가 일정 수준 (100 정도)을 지나게 되면 굉장히 marginal 한 그래프 양상을 보이며, 결국에는 향상이 일어나지 않는 수준까지 오게 되며 GA algorithm을 더 이상 사용할 필요가 없게 되어 중단을 하게 됩니다.

단, 여기서 technical 하게, 원래는 부모 세대로부터 자식 chromosome들을 만들어서 이를 평가해야 하는데, 그러다보면 수렴이 좀 느릴 수가 있기 때문에 안전장치로서 어떠한 상황을 가정해보도록 하겠습니다.

이전 세대에서 기존에 chromosome 1부터 chromosome이 100개가 있다고 가정하고, 이 중에 best가 performance 측면으로 봤을 때 top1 cheomosome이 chromosome 26이고, top2 chromosome이 chromosmosome 59라고 합니다. 그럼 다음 세대에서는 앞에서 설명을 했었던 chromosome에 대한 crossover과 mutation과정을 반복하는데, 부모 둘로부터 자식 둘이 나오기 때문에 그 과정을 50번 반복하면 100개의 새로운 chromosome이 나오게 됩니다. 다만 여기서는 아래 그림에서도 볼 수 있듯이 chromosome 26과 50은 이전 세대에서의 top chromosome이었기이었기 때문에 그냥 변형을 하지 않고 그대로 남겨둡니다. 사실 엄밀하게 말해서는 유전이 아니죠. 그냥 자기 자신이 너무 잘나서 그다음 세대에도 똑같이 살아남아있습니다. 그리고 나머지는 이전 세대의 부모들을 통해서 새로운 chromosome들을 만드는 것입니다.

그림에서 초록색은 reproduction이 된 것들을 의미하고 top1, top2는 해 수렴의 안정성을 위해서 그대로 유지를 합니다. 그 말을 무슨 얘기냐 하면, 부모세대를 뛰어넘는 자식 세대가 나오면 top1이 교체가 되겠지만 그렇지 않으면 현재 시점에서의 current best solution을 다음 세대로 끌고 가겠다는 얘기입니다.

실제 데이터에서 어떤 게 가장 잘 작동하는지 확인하기 위해 실험을 해보았습니다. 실제 Dataset은 당시 UCI machine learning repository에서 missing value가 없는 총 49개의 회귀 모형을 사용을 했고, base learner로써 선형 회귀분석을 사용했습니다.

왼쪽 그림은 원래 모든 변수들을 사용했을 때 대비 error rate가 얼마나 향상되었는지를 나타나는 것. 파란색: 원래보다 성능이 훨씬 향상, 빨강색: 저하가 있었다는 것을 의미합니다. 오른쪽 그림 variable reduction ratio를 보면, 초록색 진할수록 변수의 감소율이 높았다는 뜻이고 0으로 갈수록 변수의 감소율이 거의 없었다는 뜻입니다.

이것을 가지고 ranking을 매겨봤는데 첫번째로 error rate improvement가 좋은지 (성능 관점), 두 번째로 변수를 몇 개나 줄였느냐 (효율성 관점), 세 번째로 수행하는 시간이 얼마나 걸렸는지 (computational efficiency (효율성 관점)). 각 관점에 따른 순위는 다음과 같습니다.

GA는 예측 성능 관점에서는 가장 높은 성능을 보이고 있지만 변수를 덜 줄이고 소요되는 시간도 가장 오래 걸립니다. 그래서 방법론들에 따라서 어떤 기준을 두고 사용하느냐에 따라 장단점이 있습니다.

'Lectures > IME654: Business Analytics' 카테고리의 다른 글

[고려대학교 IME654] 01-2: Dimensionality reduction: Supervised Variable Selection (0)	2020.10.28
[고려대학교 IME654] 01-1: Dimensionality Reduction Overview (0)	2020.10.26

statigers