[고려대학교 IME654] 01-1: Dimensionality Reduction Overview

[Korea University] Business Analytics (Graduate, IME654)
1장: Dimensionality Reduction
Part 1: Overview

 

이번 포스트는 지도 학습 (supervised learning) 기반 Dimensionality reduction에 대한 내용입니다. 본 내용은 고려대학교 강필성 교수님의 2020년도 2학기 일반대학원 산업경영공학과 비즈니스 애널리틱스 (IME654) 강의를 정리하였으며, 사용된 사진 또한 수업의 강의 자료 (github.com/pilsung-kang/Business-Analytics-IME654-)를 활용하였습니다.

Dimensionality Reduction

Machine learning process는 크게 [Pre-Processing -> Learning -> Error Analysis]로 구성이 되어있습니다. 이 중 가장 첫 번째 단계인 Preprocessing 단계에서는 효율적인 Dataset 구성을 위해 Normalization, Image processing 등과 더불어 dimensionality reduction을 수행합니다.

 

Why ‘Dimensionality Reduction’? – High Dimensional Data

그렇다면 dimensionality reduction, 즉 차원 축소는 왜 해야 하는 걸까요? 우선 우리가 가지고 있는, 다뤄야 할 데이터는 대부분 고차원 데이터입니다. 예를 들어 Documentation classification을 진행할 때는 한 문서를 표현하기 위한 차원의 수가 그 언어가 가지고 있는 Token 또는 단어의 개수만큼 커졌고, Recommendation systems는 사용자 수 x item수, 예를 들어 Netflix라면 Netflix의 사용자 수와 영화와 같은 콘텐츠 개수를 곱한 값이 곧 matrix의 차원이 됩니다. 뿐만 아니라 의료 분야에서의 활용을 위해 gene expression data를 가지고 Clustering (군집분석)을 진행한다면, 해당하는 gene들의 모든 condition을 고려해야 하기 때문에 genes x conditions 만큼의 데이터가 필요하게 될 것입니다. 산업공학과로서 manufacturing 데이터를 다룰 때도 마찬가지로 고차원 데이터를 다루게 됩니다. 공정 과정은 크게 몇 가지 process로 설명할 수 있지만, 세부적으로는 수백개의 step에서 다양한 설비와 센서를 거치게 돕니다. 하지만 최종적으로 생산과정에서 발생된 불량품을 제외한 양품의 비율을 나타내는 ‘수율(yield)’을 예측함에 있어서 모든 설비와 모든 센서가 유용하지는 않을 것입니다. 그렇기 때문에 가장 효율적인 변수 집합을 찾아 나아가는 것이 중요합니다.

 

Dimensionality Reduction: Overview

Curse of Dimensionality

The number of instances increases exponentially to achieve the same explanation ability when the number of variables increases. 변수의 개수가 선형적으로 늘어날 때, 동일한 정보를 포함시키기 또는 설명하기 위해 필요한 객체 또는 샘플의 개수는 지수적으로 증가합니다.

두 점 사이의 거리가 1인 정보를 보전을 한다고 하면, 1차원에서 표현을 하려면 점 두 개만 있으면 됩니다. 2차원에서는 정사각형이 있어야 해당 정보를 보전할 수 있기 때문에 점 4개가 필요하고, 3차원에서는 정육면체가 있어야 하기 때문에 점이 8개가 필요합니다. 이걸 일반화시켜보면, d 차원의 개수에서는 2d 만큼의 점이 있어야 각 인접한 이웃 간의 거리가 1이라는 정보를 보전할 수 있게 됩니다. 그래서 첫 번째에 말씀드렸던, 변수의 개수가 증가함에 따라서 동일한 설명력을 얻기 위해서는 필요한 객체 수가 지수적으로 증가한다는 말이 설명됩니다.

데이터마이닝이나 머신러닝 관점에서 Occam's Razor의 '가장 단순한 게 가장 좋은 방법이다'라는 말이 의미하는 바는, 예를 들어 공정의 수율 예측 정확도가 90%로 같은 두 가지 경우에, 각각 sensor를 10개를 쓴 모형과 100개를 쓴 모형이 있다면, 10개를 쓴 모형을 선택하는 것이 더 낫다는 뜻입니다.

객체의 본질적인 정보를 보전하는 내재적인 차원(intrinsic dimension)의 수는 실제 original dimension보다 훨씬 적은 경우가 많습니다. 예를 들어 MNIST Dataset을 살펴보면, 기존에 16 by 16 pixel로 256 dimension이었던 데이터가 PCA와 ISOMAP을 통해 다음과 같이 2차원으로 축소된 것을 볼 수 있습니다. 2차원으로 축소 후에 시가고하가 가능해졌으며, 두 그림을 대략적으로 살펴보면 2차원으로 차원이 축소되었음에도 불구하고 각 숫자의 class는 어느정도 정확하게 구분할 수 있는 예측 능력이 있음을 알 수 있습니다.

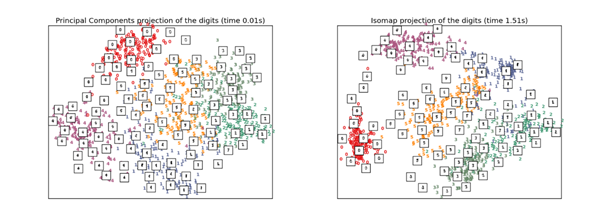
지금까지 차원이 적을 수 있다는 내용에 대해 다뤄봤다면, 이제부터는 현실 문제에서는 차원이 커질수록, 변수 개수가 많아질수록 발생할 수 있는 잠재적인 문제점에 대해 알아보도록 하겠습니다. 고차원 데이터는 다음과 같은 문제점을 발생시킵니다.

1.       개별적인 데이터에 대해서 변수가 많아질수록, 변수에 포함된 noise가 발생할 확률 또한 증가합니다.

2.       계산 복잡도가 높아집니다.

3.       동일한 일반화 성능을 얻기 위해서 더 많은 객체 수가 필요합니다.

이러한 차원의 저주를 극복하기 위해서는 다음과 같은 방법을 활용할 수 있습니다. 우선적으로 domain knowledge가 풍부한 연구자라면 일차적으로 이를 활용하여 feature를 선택할 수 있습니다. 또한 Ridge, Lasso, Elastic Net과 같은 회귀분석 기법들은 목적함수 (objective function) 자체에 regularization term을 두어서 되도록이면 적은 수의 변수를 선호하도록 설계되어 있기 때문에, 이러한 방법을 통해 변수를 선택하는 것도 하나의 방법입니다. 마지막으로 정량적인 차원축소 technique을 사용할 수도 있습니다. 이와 관련해서는 뒤에서 더 자세히 다뤄보도록 하겠습니다.

 

Dimensionality Reduction

지금까지 한 것들을 다시 한 번 정리해보면, 이론적으로 모델의 성능은 feature이 증가하면 같이 향상하는 것이 일반적입니다. 하지만 여기에는 다소 비현실적이 가정이 따르는데, 바로 ‘모든 변수들이 서로 독립이어야 한다’라는 가정입니다. 이걸 확보할 가능성은 어느 dataset에서도 굉장히 낮기 때문에, 결국 feature의 수가 증가하면 성능이 증가한다는 일반적인 이론은 그저 이론에 그치게 되는 것입니다. 현실에서는 변수 간의 의존성 (dependence), 그리고 noise가 끼어들 여지로 인해서 feature의 개수가 많아질수록 모델의 성능은 저하됩니다. 그래서 차원 축소의 목적은 모델에 대해서 가장 적합한 변수의 부분집합을 찾고자 하는 것입니다. 이렇게 상관관계가 없는 변수들을 찾아내게 되면 다음과 같은 효과가 있습니다. 우선 변수 간의 상관 관계가 없어짐으로 상관관계가 없어야 한다는 가정을 요구하는 여러 통계적인 모델을 그대로 사용할 수 있게 됩니다. 또한 사후 post-processing을 조금 더 단순화할 수 있게 되는 부분들도 있고, 중복되거나 불필요한 변수들을 제거할 수 있게 됨과 동시에, 차원이 축소되기 때문에 시각화(visualization)이 가능해집니다.

다음으로 차원을 축소하는 관점에서 몇 가지 카테고리를 살펴보도록 하겠습니다. 우선 특정한 학습 알고리즘이 차원을 축소시키는 과정에서 개입을 하는지 하지 않는지에 따라서 Supervised과 Unsupervised 방식으로 나뉘게 됩니다.

Supervised dimensionality reduction은, 어떤 데이터마이닝이나 머신러닝 모델이 사용이 돼서, 변수 선택 과정에서 깊숙하게 개입을 하는 것입니다. 다음 그림을 통해 설명할 수 있습니다.

기존 변수의 수 길이를 d라고 하고, feature selection 이후의 변수의 수 길이를 d`이라고 할 때, dimensionality reduction의 목적은 d > d`, 을 갖는 dataset을 구성하는 것이 목적입니다. 그러한 관점에서 Supervised 방식의 차원 축소의 핵심은 feedback loop가 존재한다는 것입니다. 하나의 알고리즘이 어떤 알고리즘에 대해서 특정한 변수 선택 메커니즘이 선택한 또는 추출한 변수 조합들을 평가를 해서, 더 잘해봐라, 더 잘해봐라 하는 방식으로 feedback을 줘서 loop을 계속 돌아가게 하는 방식입니다.

반면 비지도학습은 feedback loop가 없습니다. 특정한 한 가지의 비지도학습의 메커니즘을 통해서 원래 데이터의 변수의 수 (차원의 수)를 줄여주는 것을 의미합니다.

두번째로는 변수(차원)을 축소한다는 관점에서 봤을 때 또 하나는, 축소된 결과물이 무엇이냐에 따라서 두 가지로 구분할 수 있습니다. 1) Variable/feature selection 2) Variable/feature extraction

우선 variable/feature selection은 원래 original 변수들 중 유의미할 것으로 판단되는 부분집합을 명시적으로 선택하는 방법이고, 원래보다 더 적은 개수의 변수를 선택하게 됩니다. 어떠한 기준에 의해서 original 변수에서 몇 개를 남겨 ‘부분집합’을 이루게 된 것입니다.

반면 variable/feature extraction은 특정한 메커니즘에 의해서 새로운 변수들을 만들어냅니다. 아래의 표에 보면 variable selection 같은 경우에는 기존과 같은 X 변수가, variable extraction의 경우에는 X가 아니라 Z라는 새로운 변수가 만들어진 것을 확인할 수 있습니다.

이어서 Feature Selection과 Feature Extraction의 Technique에 대해서 자세히 다뤄보도록 하겠습니다.

Feature Selection 방식은 크게 Filter 방식과 Wrapper 방식이 있는데, Filter는 알고리즘을 사용하지 않고 특정한 메커니즘에서 한 차례 변수를 선택하기 때문에 unsupervised 방식에 가깝습니다. 반면 Wrapper 방식은 feedback loop이 있는 supervised dimensionality reduction 방식에 해당되며, Forward/Backward/Stepwise/Genetic algorithm이 Wrapper 방식에 해당됩니다.

Feature Extraction은 class label이라는 정보를 전부 사용하지 않고, learning algorithm 또한 사용하지 않습니다. 그렇다면 어떻게 차원을 축소할 수 있냐 하면, 데이터가 가지고 있는 본질적인 정보를 가장 최대한으로 보존하는 방식으로 변수를 줄여 나갑니다. 결국 핵심은 데이터가 가지고 있는 본질적인 정보가 무엇이냐는 질문으로 귀결될 수 있는데, 여기 등장하는 세 가지 technique으로 설명할 수 있습니다. 우선 첫번째는 variance(분산)을 최대화하는 통계에서 많이 다뤘을 주성분분석 (PCA), 객체 간의 거리 정보를 최대화하는, 사회과학 분야에서 많이 사용되는 다차원 척도법(Multidimensional scaling)이 있습니다. 앞서 설명한 방법들이 모두 선 형 변환인데, 선형이 아닌 비선형 변환(hidden structure)을 찾아내는 방식이 non-linear structure입니다. LLE, ISOMAP, t-SNE가 비선형 변환에 해당됩니다.

설명한 기법들 중 Filter 방식을 제외하고는 모두 자세히 다룰 예정입니다.

 

Dimensionality Reduction: Recent Trends

Representation Learning: Deep Auto-Encoder

Representation learning에는 대표적으로 Deep auto-encoder가 있습니다. auto-encoder는 데이터를 가져다가 원래 이미지가 그대로 다시 나오도록 decoding을 진행하고, 이 과정에서 encoder과 decoder를 거쳐가게 됩니다. 여기서 bottleneck layer (30이라고 표시된 부분)을 줘서, 원래 이미지보다 차원을 줄이는 작업을 진행하도록 합니다. 그림을 통해서 기존 고차원 이미지 데이터를 30차원의 정보로 줄인 것을 확인할 수 있으며, 여기서 줄인 latent vector가 정보를 보존합니다.

논문 Recommendation (꼭 읽어볼 것): Bengio, Y., Courville, A., & Vincent, P. (2013). Representation Learning: A Review and New Perspectives. IEEE transactions on pattern analysis and machine intelligence, 35(8), 1798-1828

MNIST Dataset에도 다음과 같은 방법으로 autoencoder를 적용시킬 수 있다.

(a) input을 (b) reconstruction 이미지처럼 자기 자신을 복제하기 위해서 h를 가지고서라도 x라는 input이 어느정도 복원이 된다면, 정보가 어느정도 효율적으로 압축이 된 representation이라고 볼 수 있다. 그럼 x대신 h를 사용해도 무방하다는 말이 되는 것이다.

 

Representation Learning: De-noising Auto-Encoder

Auto-Encoder는 Noise에 워낙 민감하다. 그렇기 때문에 본 모델은 입력에 노이즈를 첨가해도 노이즈가 제거된 결과값이 나오도록 설계되었다. Noise는 Gaussian Noise를 일반적으로 사용하여 생성되었다.

Representation Learning: Convolutional Neural Network (Convolutional Auto-Encoders)

CNN을 통해서 feature extraction을 진행할 수 있다. 28 by 28의 고차원 데이터를 10차원의 vector로 변환할 수 있다. 이때 이 vector는 핵심 정보를 전부 내포하고 있으며, 이 layer는 저차원의 hidden state가 되는 것이다.

Representative Learning: Word/Document Embedding

다음과 같은 기술들도 모두 representation learning의 흐름 중 일부다.

Representative Learning: Pre-trained models

논문: Jacob Devlin, Ming-Wei Chang, Kenton Lee, Kristina Toutanova. (2018). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding, arXiv preprint arXiv:1810.04805.

Pre-trained model이라고 해서, 자연어 (NLP) 분야 같은 경우에는 Scratch로 처음부터 모델을 학습해서 representation을 사용하는 게 아닌, 이미 만들어져 있고 배포된 (사전에 학습된) 모델에서 필요한 부분만을 따오는 그러한 형태도 가능합니다.