[고려대학교 IME654] 01-2: Dimensionality reduction: Supervised Variable Selection
[Korea University] Business Analytics (Graduate, IME654)
1장: Dimensionality Reduction
Part 2: 변수 선택 기법: 전진 선택법, 후방 소거법, 단계적 선택법
이번 포스트는 지도 학습 (supervised learning) 기반 Dimensionality reduction, 즉 변수 선택 기법에 대한 내용입니다. 본 내용은 고려대학교 강필성 교수님의 2020년도 2학기 일반대학원 산업경영공학과 비즈니스 애널리틱스 (IME654) 강의를 정리하였으며, 사용된 사진 또한 수업의 강의 자료 (github.com/pilsung-kang/Business-Analytics-IME654-)를 활용하였습니다.
Exhaustive Search (전역 탐색)
변수 선택 (feature selection)은 우리가 가지고 있는 전체 변수들 중에서 일부분의 유효한 변수를 찾아내는 것입니다. 이때 변수를 변환하거나 치환하지 않고 기존에 가지고 있는 변수들 중 선택을 하게 됩니다. 예를 들어 아래와 같이 세 개의 변수 $x_1, x_2, x_3$를 가지고 모든 subset 조합을 찾으려고 할 때, 가능한 모든 조합을 만든다면 총 7가지 조합이 나오게 됩니다. 최종적으로 이 조합들 중 가장 성능이 좋은 조합을 사용하면 됩니다. 성능 평가지표는 다양한데, AIC, BIC, $R^2$ 값 등 모델에 따라 각기 다른 기준을 사용하면 됩니다.
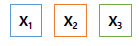

하지만 현실적으로 위와 같이 변수들이 생성해낼 수 있는 모든 subset을 찾아낸 후 그 중 가장 성능이 좋은 subset을 고르는 방식은 불가능합니다. 아래 그래프는 변수의 개수에 따라 늘어나는 model의 개수를 표현한 것입니다. 중요한 것은 이 단위가 log scale이라는 것이며, 오른쪽 축에는 1초에 10,000개의 모델을 평가할 수 있는 컴퓨터를 사용했을 때 소요되는 시간이 표기되어 있습니다. 즉 초당 10000개의 모델을 evaluate할 수 있는 컴퓨터를 가지고 있다 하더라도, 전역 탐색
(연두색 그래프)을 하게 되면 변수가 약 20개 일 때 1분이 소요되고, 40개가 되지 않았는데도 하루가 걸린며, 변수 40개를 평가하기 위해서는 1년이라는 시간이 소요되기 때문에 현실적으로 전역 탐색 방법은 변수 선택 방법으로서 사용이 불가능합니다.

다만, 전역 탐색을 통해 변수를 선택하면, 가능한 모든 조합들 중 가장 좋은 걸 찾아주기 때문에 항상 최적의 subset, 즉 global optimum을 찾을 수 있게 됩니다. 그래서 전역 탐색을 기준으로 성능의 저하 최소화, 소요시간 단축 최대화를 하는 지도 학습을 기반으로 하는 대표적인 변수 선택 기법들인 Forward Selection (전진선택법), Backward Selection (후방소거법), Stepwise Selection (단계적 선택법)에 대해서 알아보도록 하겠습니다. 이러한 기법들의 목적은 변수 선택에 소요되는 시간을 전역탐색에 비해 최대한 줄이고, 변수 선택 기법에 의해서 선택된 변수 조합들을 이용해서 만든 예측되는 성능은 전역탐색과의 차이가 최소화되도록 하는 것입니다.이 technique들은 특정 알고리즘에 종속적인 것이 아니기 때문에 모든 supervised learning에 사용될 수 있습니다. 다만 이 강의에서는 설명의 용이성을 선형회귀 모형을 사용하였습니다.

Forward Selection (전진선택법)
Forward selection은 아무것도 없는 모델에서부터 시작을 해서 변수가 하나씩 추가되는 과정을 거치게 됩니다. 평가 지표의 향상을 보였을 때만 변수를 추가할 수 있으며 변수가 한 번 선택되면 절대 제거되지 않습니다.

아래 예시는 8개의 입력 변수를 모두 확인해보는 방식으로 진행이 됩니다. 평가지표는 조정된 $R^2$ 값인 $R_adj^2$을 사용하였으며, 8개의 입력변수를 넣었을 때 나온 평가 지표의 값들 중 가장 우수한 값을 내는 변수를 첫번째로 선택합니다.그 다음으로는 $x_2$를 고정을 하고, 다른 변수를 하나하나씩 조합해가면서 두개의 변수로 이루어진 회귀분석 모형을 만들어갑니다. $x_2$를 고정한 상태에서 $R_adj^2$값이 가장 큰 모형은 $x_2$와 $x_7$이 조합되었을 때가 된다. 다음으로 $x_2$와 $x_7$을 조합하고 모든 변수르 넣어본 뒤 $R_adj^2$값을 다시 한 번 비교해서 가장 높은 $R_adj^2$값을 가지고 있는 모형을 선택한다. 이 과정을 반복적으로 진행하다보면, 마지막 사진에서 보이는 것과 같이 $R_adj^2$값이 이전 단계에서보다 향상이 되지 않는 시점이 된다. 이때 forward selection을 중단하고 final model을 선택하게 된다.

Backward Selection (후방소거법)
Backward elimination은 forward selection과 정반대의 개념을 가지고 있습니다. 모든 변수를 사용한 모델에서부터 시작을 해서 중요하지 않은 변수들을 하나씩 제거합니다. 중요하지 않은 변수를 정하는 기준은, 특정 변수를 제외했는데도 성능 지표의 하락이 없거나 아주 미미한 경우를 뜻합니다. '성능지표의 하락이 없다'를 기준으로 잡으면 지나치게 엄격하기 때문에 하락이 특정 값 미만이면 제거한다는 기준을 정합니다. 변수가 한 번 제거가 되면 절대 다시 선택될 가능성이 없습니다.

이전 예시에서 사용했던 예제를 가지고 backward elimination을 진행했습니다. 8개 변수를 모두 넣었을 때의 $R_adj^2$값은 0.77이 나왔습니다. 그 다음, 변수를 하나씩 제외시켜 봅니다. $x_3$를 제외했음에도 불구하고 $R_adj^2$값은 0.77에서 0.77로 변화가 없었습니다. $x_3$는 모형을 만드는 데 의미가 없다는 걸 알 수 있기 때문에, $x_3$를 제거합니다. $x_3$를 제거한 상태에서 남은 변수들을 하나씩 모두 제외시켜 봅니다. 마지막 변수인 $x_8$을 제외시키니 기존 $R_adj^2$값인 0.77과 0.01 차이가 나기 때문에 미미한 차이라고 판단하고 $x_8$을 제거합니다. 모든 변수가 있었던 모형에서의 $R_adj^2$값은 0.77, 그리고 $x_3$과 $x_8$을 제외시켰는데도 불구하고 여전히 $R_adj^2$값은 0.76으로 0.01밖에 떨어지지 않았습니다. 이어서 $x_3$과 $x_8$을 제거한 모형 상태에서 나머지 변수들을 한 번씩 제외시켜 봅니다. 현재 모델의 $R_adj^2$ 값인 0.76과 비교했을 때, 어떠한 변수를 제거하더라도 급격한 $R_adj^2$값의 변화가 일어남으로 더이상 변수를 제거하지 않고 backward elmination은 종료가 됩니다.
Stepwise Selection (단계적 선택법)
우리는 global optimum을 찾아주는 전역탐색이 사실상 사용이 불가능하기 때문에 성능을 최대한 유지하면서 소요시간을 매우 크게 단축하는 기법인 Forward Selection과 Backward Elimination입니다. 다만 소요시간은 변수의 개수에 비례하기 때문에, forward selection의 탐색 영역이 기존 전역탐색보다 훨씬 좁아질 수밖에 없고, 이에 필연적으로 성능 저하가 발생합니다. 그래서 성능을 조금 더 향상시키고자 하는 목적을 가진 변수선택 방법이 바로 Stepwise selection 방법입니다. Stepwise Selection은 forward selection과 backward elimination을 번갈아 사용하면서 더 최적의 조합을 찾기 위해 소요 시간을 조금 더 들입니다. 그리고 forward selection과 backward elimination과 다르게 한 번 선택되었다고 해도 제거될 수 있고, 한 번 제거 되었어도 다시 선택될 수 있습니다.

앞선 예시와 비슷하게 설명해보도록 하겠습니다. 우선 첫번째로 forward selection을 수행하면, 변수 $x_2$를 선택하게 됩니다.

그 다음에 이제 backward elimination으로 변수를 제거하게 되는데, 변수 $x_2$는 제거가 되면 원 상태 (아무것도 없는 모델)과 같아지기 때문에 제거가 되지 않습니다. 그 다음 다시 forward selection을 수행하여 변수 $x_7$을 선택합니다.

그 상태에서 다시 backward elimination을 시도합니다. 이때 어떤 변수를 제거할지 결정할 때는 다음 두 식을 비교합니다.

다만 두 시을 살펴보면, 변수 하나를 추가한 상태에서 forward selection을 진행할 때 위의 모형보다 아래 모형이 $R_adj^2$값이 더 높았기 때문에 첫번째 forward selection 단계에서 선택되었을 것입니다. 또한 변수 하나가 추가된 모델보다 현재의 변수 두 개가 있는 모델이 당연히 더 우수한 모델이기 때문에 하단 식도 선택되지 않습니다. 그래서 여기서도 역시 마찬가지로, backward elimination 과정에서 어떤 변수도 제거되지 않게 됩니다. 다음으로 세번째 변수를 forward로 선택을 하게 되면, $x_4$ 변수가 선택되면서 $R_adj^2$값이 0.76으로 향상됩니다.
여기서 이제 forward와 stepwise의 차이가 나오게 되는데, 이 다음 단계에서 backward로 변수를 제거하는 시도를 해봅니다. 이때 다음과 같은 세 가지 조합을 고려하게 되는 것인데, 이 중 변수 $x_4$와 $x_7$을 고려하는 마지막 모형은 기존 forward selection 단계나 backward elimination 단계에서는 고려될 수 없었던 모형입니다. 극단적인 예시지만, $x_4$와 $x_7$가 개별적 성능으로 보았을 때는 $x_2$보다 좋지 않았지만, 이 둘을 조합했을 때는 가장 좋을 수도 있습니다. 그럼 x2가 첫번째로 선택 되었음에도 불구하고 이 단계에서 제거가 될 수 있다는 뜻입니다. 그래서 forward에서는 고려할 수 없었던 상황을 stepwise에서는 허용되기 때문에, 과감하게 첫번째로 선택한 변수인 $x_2$를 제외할 수 있게됩니다.

더 이상 어떠한 변수도 새롭게 선택되거나 제거되지 않을 때까지 이러한 step을 반복합니다.

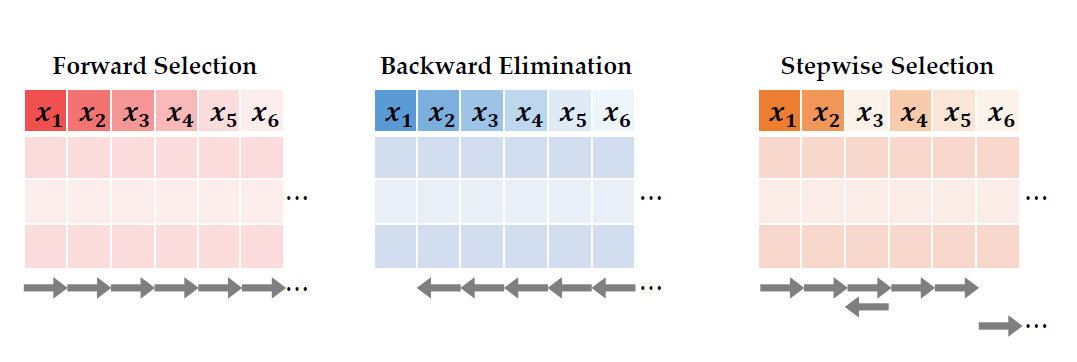
Forward Selection은 증가하는 방식, Backward Elimination은 줄어드는 방식, Stepwise Selection은 늘었다 줄었다 하는 방식이라고 이해할 수 있습니다.
Performance Metrics
이러한 변수 선택을 하는 데에 있어서, 회귀 모형을 평가할 때는 AIC나 BIC, $R_adj^2$과 같은 지표들이 사용될 수 있습니다. 다만 이러한 평가지표들은 모두 회귀 모형에 적합한 모델이고, 보다 더 일반적인 평가 지표는 변수 선택을 하기 위한 검증용 데이터를 세팅을 해놓고, 검증 데이터에 대한 분류/회귀 평가 지표를 사용하는 것이 일반적이라고 볼 수 있습니다.